ФЛУОРЕСЦЕНЦИЯ ПРИ АНИЗОТРОПНОМ ПЕРВИЧНОМ РЕНТГЕНОВСКОМ ИЗЛУЧЕНИИ
Аннотация
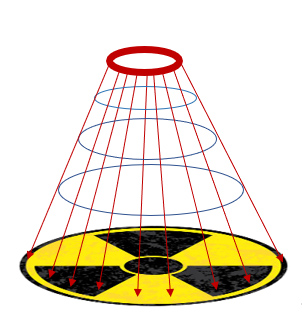
При рентгеноспектральном флуоресцентном анализе анизотропия первичного излучения приводит к неравномерному облучению поверхности образца, усиливая роль одних участков и ослабляя роль других. Целью работы явилось определение минимального расстояния от окна рентгеновской трубки с конусным анодом, на котором интенсивность облучения образца становится однородной. Метод исследования состоял в моделировании на ЭВМ рентгенофлуоресцентного эксперимента. Рабочая модель была построена на основе двух формул для плотностей потока тормозного и характеристического излучений массивного анода, в которых учтено поглощение первичного излучения в материале анода и обратное рассеяние электронов. Кольцевой источник в модели представлялся суммой бесконечно малых линейных элементов одинаковой мощности, образец имел форму диска соосного источнику. Расчетная диаграмма удачно согласуется с известной из литературы экспериментальной диаграммой направленности излучения. Рассчитывалось два пространственных распределения. Первое описывало распределение интенсивности первичного излучения по поверхности образца, второе – распределение флуоресцентного излучения, которое имеет большую ценность для рентгеноспектрального анализа. Расчет показал, что хотя, в отличие от первого, второе распределение учитывает поглощение первичного излучения и вторичного излучения в образце, оба распределения оказались близкими по форме. Показано, что область пробы, несущая большую часть информацию о составе облучаемого образца, имеют форму кольца, ширина которого зависит от расстояния до окна рентгеновской трубки. По мере его увеличения диаграмма пространственного распределения интенсивности излучения сглаживается и на расстояниях больших двух диаметров анода излучение становится однородным. Полученная в работе модель, учитывающая анизотропию первичного излучения, может быть применена в методе фундаментальных параметров рентгенофлуоресцентного анализа для спектрометра со сжатой геометрией.
Ключевые слова: конусный анод, диаграмма направленности рентгеновского излучения, флуоресценция
Полный текст:
PDF (Russian)Литература
REFERENCES
Afanasiev I.B., Danichev V.V., Ivanov V.F., Kondratenko R.I., Mikhin V.A. Use of fundamental parameters method for quantitative analysis of spectra acquired on spectrometer with Kumakhov lens. X-ray and Neutron Capillary Optics II, edited by Muradin A. Kumakhov, Proc. of SPIE Vol. 5943. 59430O-1 (2006). doi: 10.1117/12.637977
Volkov V.F., Mironenko M.Iu. [Calculation of the spatial distribution of X-ray fluorescent radiation of an extended source]. Apparatura i metody rentgenovskogo analiza [Devices and Methods of X-ray Analysis], Leningrad, 1988, vol. 38, pp. 36-39 (In Russian).
Sherman J. The theoretical derivation fluorescent X-ray intensities from mixtures. Spectrochimica Acta, 1955, vol. 7, pp. 283-306. doi: 10.1016/0371-1951(55)80041-0
Losev N.F. Kolichestvennyi rentgenospektral`nyi fluorestsentnyi analiz [Quantitative X-ray fluorescence analysis]. Moscow, Nauka, 1969, 336 p. (In Russian).
Criss J.W., Birks L.S. Calculation methods for fluorescent X-Ray spectrometry. Empirical coefficients v.s. fundamental Parameters. Analytical Chemistry, 1968, vol. 40, no. 7, pp.1080-1086. doi: 10.1021/ac60263a023
Afonin V.P., Finkelshtein A.L., Borkhodoev V.J. and Gunicheva T.N. X-Ray Fluorescence Analysis of Rocks by the Fundamental Parameter Method. X-Ray Spectrometry, 1992, vol. 21, pp. 69-75. doi: 10.1002/xrs.1300210205
Kitov B.I. Calculation Features of the Fundamental Parameter Method in XRF. X-Ray Spectrometry, 2000, vol. 29, pp. 285-290. doi: 10.1002/1097-4539(200007/08)29:4<285::AID-XRS428>3.0.CO;2-C
Pavlinsky G.V., Kitov B.I. Influence of divergence of the Primary radiation beam on the line intensity of the X-Ray fluorescence spectrum. X-Ray Spectrometry, 1979, vol. 8, no. 3, pp. 96-101. doi: 10.1002/xrs.1300080303
Ivanov S.A., Maksimov V.M., Nikolaenko G.M., Shchukin G.A. [X-ray tubes for fluorescent spectral analysis]. Apparatura i metody rentgenovskogo analiza [Devices and Methods of X-ray analysis], Leningrad., 1980, vol. 23, pp. 139-141. (In Russian).
Finkelshtein A.L., Gunitcheva T.N., Afonin V.P., Paradina L.F., Piskunova L.F. [Calculation of spectral distribution of primary radiation in X-ray fluorescent analysis]. Zavodskaia laboratoriia [Factory Lab], 1981, vol. 47, no. 11, pp. 28-31 (In Russian).
Kramers Н.А. XCIII. On the theory of X-ray absorption and of the continues X-ray spectrum. Рhyl. Маg., 1923, vol. 46, no. 275, pp. 836-871. doi: 10.1080/14786442308565244
Philibert J. A method for calculating the absorption correction functions for electron probe microanalysis. Х-Rау Oрtic аnd X-Ray Microanalysis, 1963, pp. 379-392.
Reed S.J.B. Electron Microprobe Analysis. Cambridge London, Cambridge University Press, 1975, 424 p.
Afonin V.P. X-ray fluorescence analysis of rocks. Fresenius Z. Anal. Chemistry, 1989, no. 335, pp. 55-57. doi: 10.1007/BF00482392
Каgаn B.S., Lapenko V.V., Levitin A.L., Frumkin S.P. [Spatial distribution of the intensity of radiation of X-ray tubes of BKHV-6 and BKHV-7 types]. Apparatura i metody rentgenovskogo analiza [Devices and Methods of X-ray analysis], Leningrad, 1981, vol. 25, pp. 39-41 (In Russian).
Kasianov P.M. Rentgenofizicheskii analiz neorganicheskikh veshchestv slozhnogo khimicheskogo sostava [X-ray physical analysis of non-organic substances of complex chemical composition]. Tiumen, TIU, 2016, 195 p. (In Russian).
DOI: https://doi.org/10.15826/analitika.2022.26.1.002
Ссылки
- На текущий момент ссылки отсутствуют.
